Bloom Filter

布隆过滤器是一种概率性的数据结构，主要用于判断一个元素是否出现过。

对于检查一个元素是否出现过的简单实现可能只需要使用 Set。考虑一种场景，假设我们想检查一个用户是否是第一次访问我们的网站，那么使用 Set 的简单实现如下：

class VisitorTracker:
  def __init__(self):
    self.visitors = set()
    
  def add_visitor(self, user_id):
    self.visitors.add(user_id)
    
  def has_visited_before(self, user_id):
    return user_id in self.visitors

visitor_tracker = VisitorTracker()
visitor_tracker.add_visitor("user_a")
visitor_tracker.add_visitor("user_b")
visitor_tracker.add_visitor("user_c")

visitor_tracker.has_visited_before("user_a")  # True
visitor_tracker.has_visited_before("user_d")  # False

上述实现只是对 Set 的简单包装；对于简单的场景来说，能够很好地运行，但是考虑到如果我们逐渐有大量的用户访问网站，会发生什么情况？该实现意味着底层的 Set 必须记住所有已经出现的用户信息；那么当越来越多的用户访问网站，我们的内存空间使用会呈线性增长。

在我们处理这些类型问题的时候，我们通常不会关心 100% 的准确性（如果我们没有给每一个新用户展示特别的 Banner 是否特别重要？大概率不是很重要）。布隆过滤器能够帮助我们解决这种不是严格要求的问题，同时能够限制我们的内存使用率以换取偶尔的误报。这正是布隆过滤器的优势。

布隆过滤器是通过一个位数组（bit array）来实现的；同时会包含几个 Hash 函数，每个 Hash 函数以一个元素值作为参数，同时返回一个位数组（bit array）索引。通常来说，位数组会比较大（用于减少冲突的概率）。下面是一个长度为 20 的例子：

假设我们的布隆过滤器使用三个 Hash 函数（h1, h2, h3）。把元素值 a 分别传给这三个函数，会产生三个不同的位数组索引。那么，插入一个元素意味着将这三个索引位置的位由 0 翻转成 1。

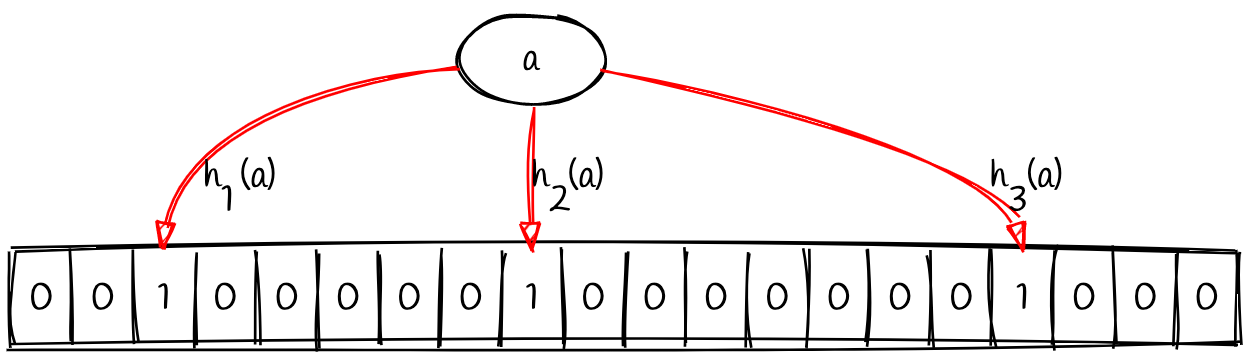
同样，当我们插入其他值（b, c）后，布隆过滤器中的位数组可能看起来如下：

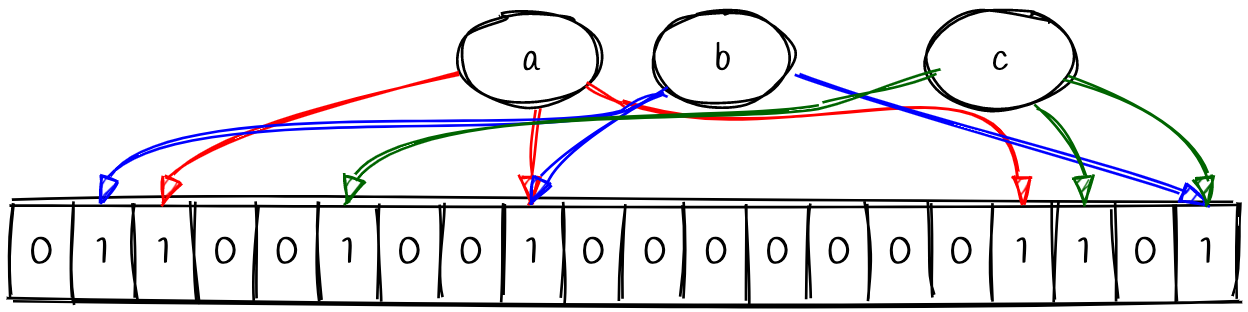
注意到，元素的插入产生了一些冲突（元素 a 与 b 在位数组中部有冲突，元素 b 与 c 在位数组的右侧有冲突）。这是正常现象，这就是布隆过滤器的部分概率性的原因。

数据已经插入完成了，那么我们如何判断一个元素是否已经出现了呢？首先，我们的 Hash 函数是确定的，所以对于同样的元素值，Hash 函数总是能返回同样的索引位置。接下来我们使用刚才的布隆过滤器判断元素 b, d 是否出现。

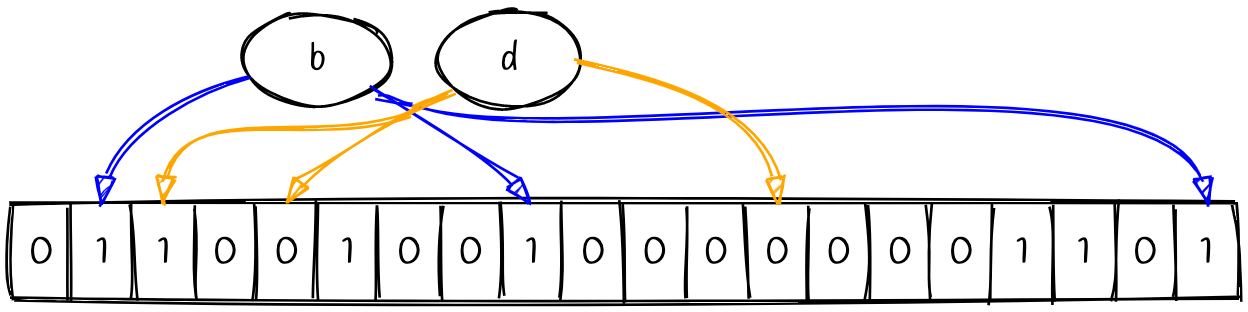
元素 d 的索引有两个位置并没有被翻转成 1；正是因为元素 d 的索引位置中存在并没有置为 1 的情况，那么我们可以肯定元素 d 之前没有出现过。

对于元素 b，其对应的三个索引位置均被翻转成 1，那么我们不能判断 b 一定出现过，只能说 b 可能出现过。至于为什么不能肯定 b 出现过，考虑一个新的元素 e.

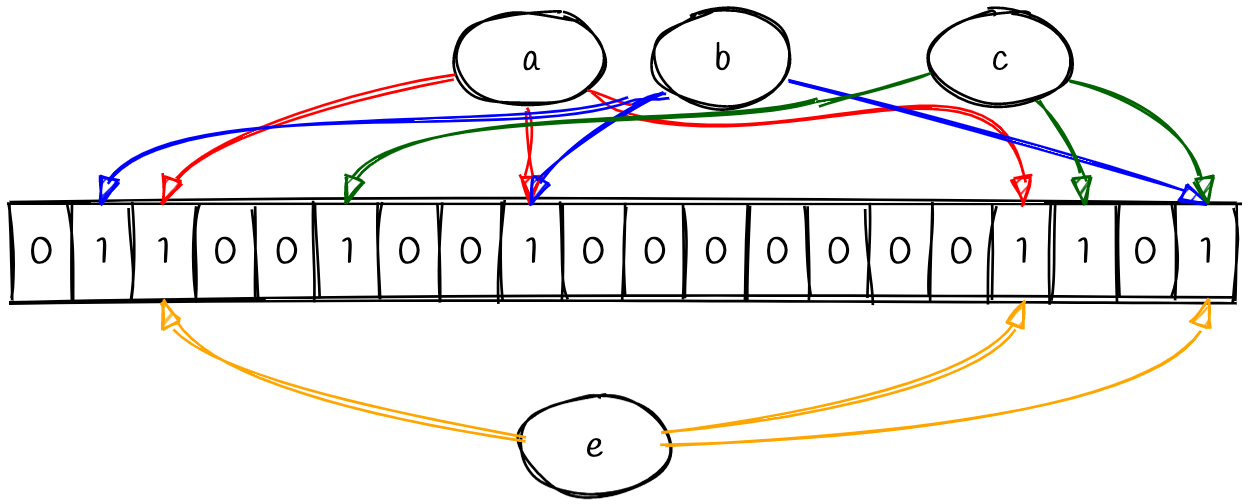
我们之前并没有插入元素 e，但是其 Hash 索引对应的位置均被翻转了；这是因为 e 元素的索引与之前插入元素的索引位置产生了冲突。

这个现象表明，我们可能会遇到假阳性（false positive），所以我们只能说元素可能出现过；相反，布隆过滤器并不会表现出假阴性（false negative），这是因为我们的 Hash 函数是确定的，如果某个元素之前出现过，那么其对应的索引位一定会被翻转。

通常来说，如果我们使用的位数组比较大的话，冲突的概率是比较小的。我们可以指定位数组的大小，Hash 函数的数量来实现特定的布隆过滤器。